Overview
The Unit Root Test provides you with a tool to test if a series is non-stationary. More specifically, it performs an Augmented Dickey-Fuller (ADF) test of the null hypothesis that a time series has a unite root, which will violate the underlying assumptions in many statistical models. The analysis produces a report in which you can read and interpret results from the statistical test.
Estimation model
If a unit root is present in the system, the variance may be infinite overall and the data can be difficult to use in further analysis. The ADF test regression equation has the form:
is the coefficient of the endogenous variable y on level form and is used for the actual test. Viewed as an autoregressive process, AR(p), the -coefficients are for the p lags of y on difference form, . The ADF test (Dickey & Fuller, 1979) introduced lagged differenced variables to whiten the residuals, e, in the estimation. The lag length, p, should be chosen carefully observing the change in information criterion and should apply to the AR-model regardless of whether it has a unit root. (Sometimes t-values are used as criteria instead.) If an AR(1) process is assumed, all -terms can be omitted by setting both min and max lag to zero, given that e is still trusted to be approximately white noise. is the coefficient for the constant term and for the linear trend.
If the series is assumed to be integrated, it can be differenced by checking the diff box. Note that trend and constant terms are not affected by this.
The null hypothesis is that the series has a unit root, so that is equal to zero, or:
Evaluation is done with t-values from the sample statistics, after OLS estimation. Because the t-values of the ADF estimator are non-standard both in sample and asymptotically, special tables and response surface calculations from MacKinnon 1996 are used (with permission) to calculate the p-value. The settings for the deterministic variables are in a drop-down box. The MacKinnon calculations will adjust to this (and to sample size) automatically but cannot account for other deterministic (or exogenous) variables, so MB does not allow them in the ADF test.
References
Dickey, D. A., and Fuller, W. A. (1979), “Distribution of the Estimators for Autoregressive Time Series with a Unit Root,” Journal of the American Statistical Association, 74, 427-431
MacKinnon, James G, 1996. "Numerical Distribution Functions for Unit Root and Cointegration Tests," Journal of Applied Econometrics, John Wiley & Sons, Ltd., vol. 11(6), pages 601-618, Nov.-Dec.
(Programs and files: http://qed.econ.queensu.ca/pub/faculty/mackinnon/numdist/)
Settings
Start Lag/End Lag
To perform the analysis, you must specify which number of lags that will be included in the test. If you change 'Start lag' to 1 and 'End lag' to 3, it will include lags of 1, 2 and 3 in the test. It is also possible to run the test in a classical Dickey Fuller setup, without any lagged differences, by setting both min and max lag to zero.
Include
Select if you want to include this series in the analysis.
Diff
By selecting Diff, the first order differences of the series will be calculated. The result will then be converted back to levels. First order of differences means that the series is transformed to "Change in value" (one observation) while expressing the result in levels.
Deterministic variables
Select if you want to include any deterministic variables in the equation, intercept or intercept and linear trend.
Report
The Unit Root Test automatically generates a report, which includes a variety of statistical information.
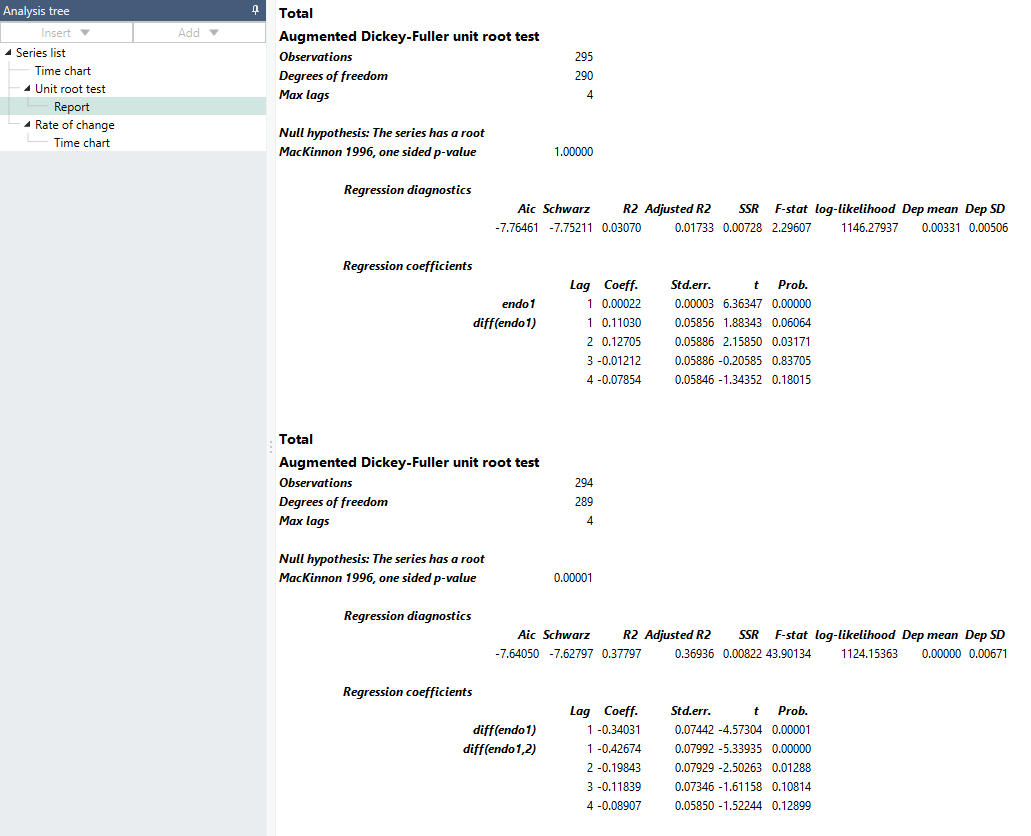
Examples
In this example, we used the Unit Root Test on the U.S. GDP, expressed in logarithm. One version of the series has been expressed in differentials, to see how results would differ.
Questions
If I’m getting p < 0.05 does that mean series has unit root or not?
A p-value close to 1 indicates that there is likely a unit root. If there is a unit root, the series is not stationary.
A p-value closer to 0 means that we can likely reject the assumption that there is a unit root and the series is stationary.