Overview
The Rolling principal components analysis (Rolling PCA) allows you to calculate a set of linearly uncorrelated series, or components, from a set of possibly correlated series. Rolling PCA enables you to do a time-dependent calculation which uses a moving or expanding window to compute the calculation.
For information about not-rolling version of this analysis see Principal components analysis.
Settings
General
Do not include series used in calculations in the output
When checked, any series included in the calculation will be excluded from the output. Uncheck this setting if you want both the original series and the calculation result in the output.
Include new series automatically
When checked, any new series added to the Series list will automatically be included in the calculation.
Select method for creating matrix
Use correlation (normalize input)
The eigenvectors will be calculated from the correlation matrix. This means that the input is centered and normalized before the components are calculated. PCA is sensitive to the scale of the input. Therefore, use this setting if variables are of different units, e.g., currencies and indices.
Use covariance
The eigenvectors will be calculated from the covariance matrix. This means that the input is only centered before the components are calculated. Remember that if you choose covariance, the input is not normalized, and the analysis will be sensitive to the scale of the input.
Select window type
Use expanding window
Observations will be added successively to the calculation one at the time from the beginning of the start date to the last observation available.
The calculations will start when there are as many observations as there are components.
Use moving window
The analysis will be performed on a specified window of observations that moves forward one observation at the time. Check this setting if you want to set the length of the moving window.
The window size cannot be smaller than the number of components and the calculations will start when there are enough observations to fill one window.
Output
Output: Eigenvalues/Cumulative proportions
The output is either the eigenvalue of each principal component of each window as we 'roll' over the input series or the cumulative proportions of the captured variance. The output will thus be as many time series as input series.
Output series description
Specify the description of the output series or use the default description.
Include
Select what series to include in the calculation.
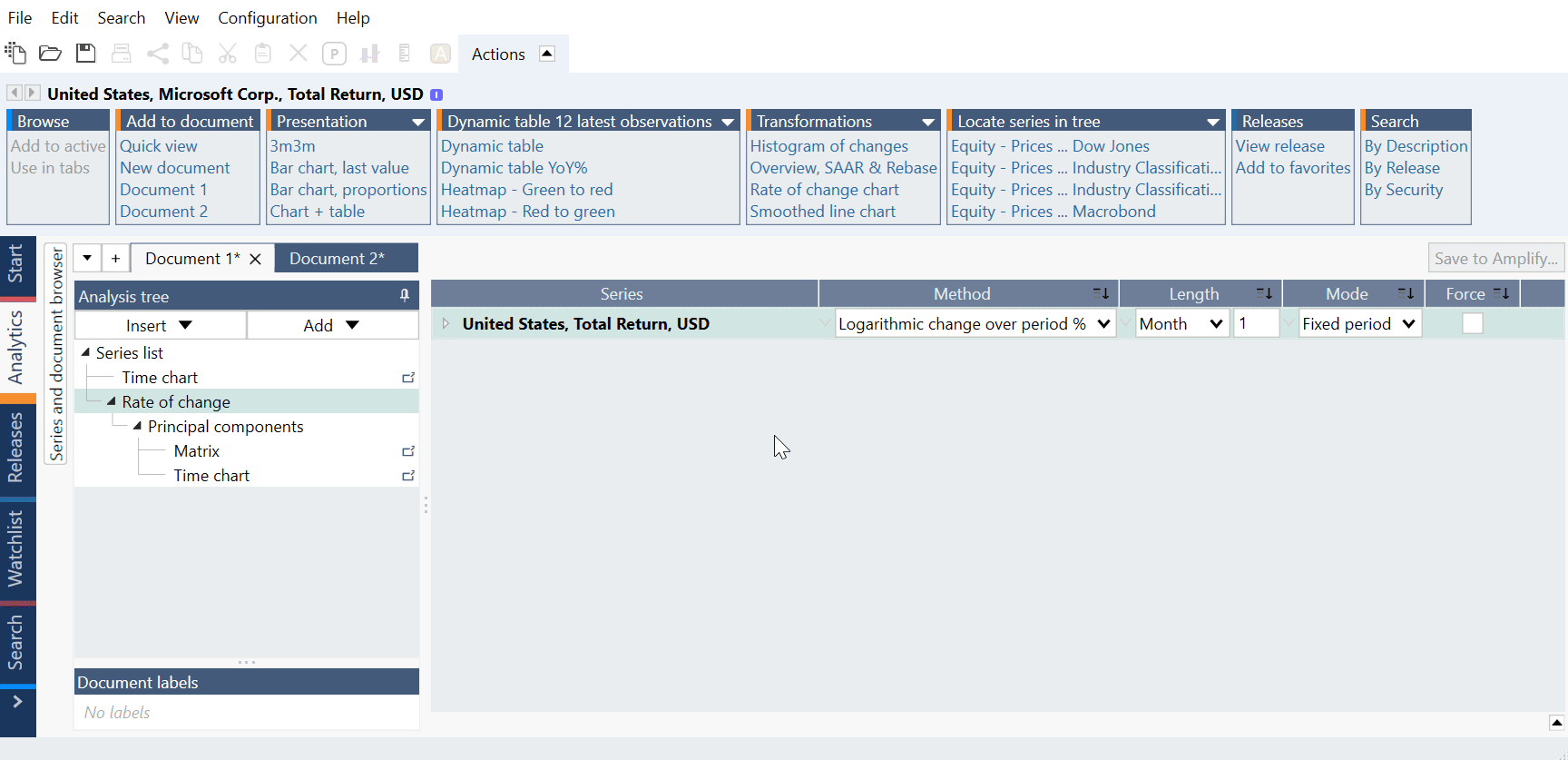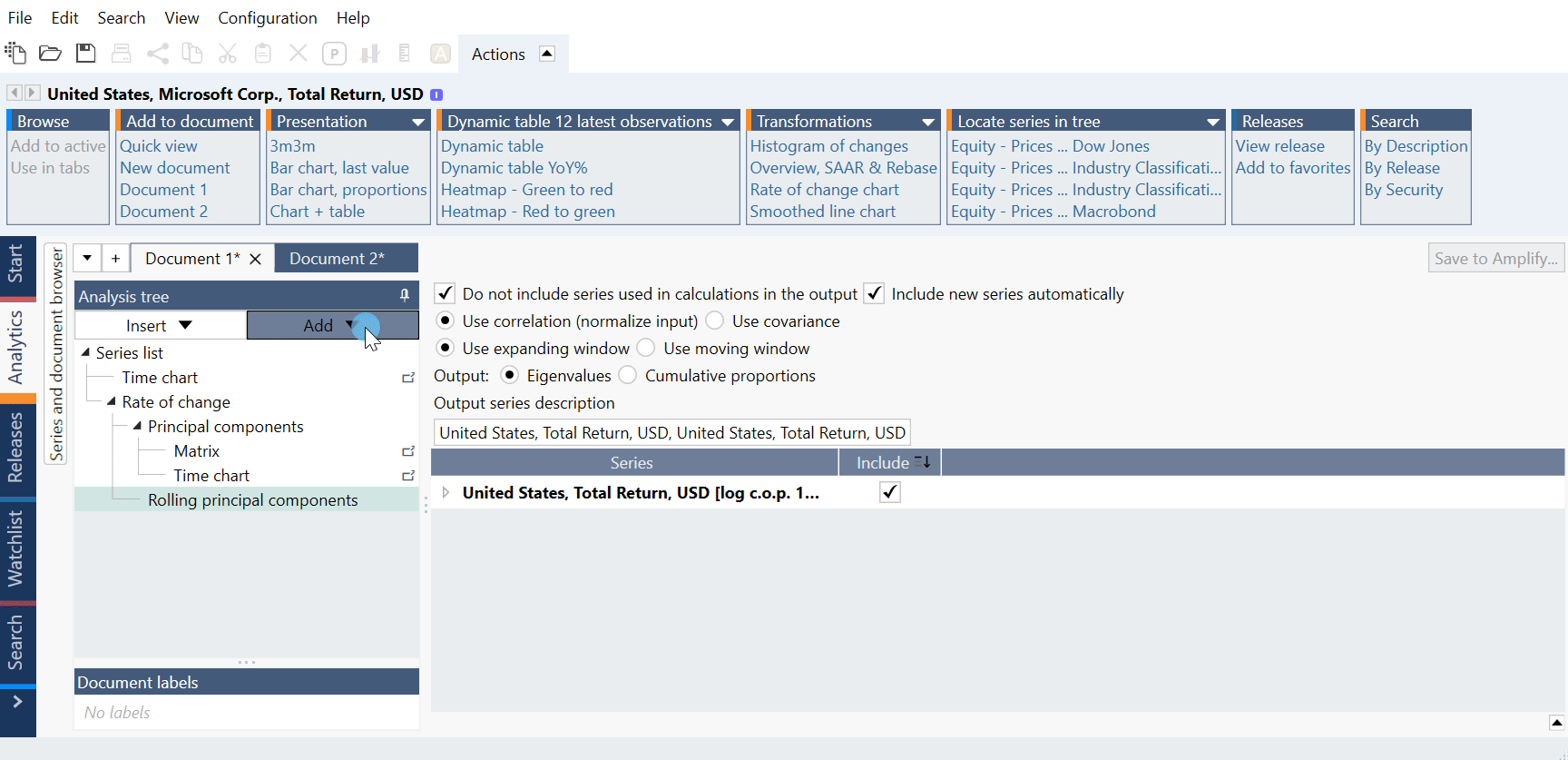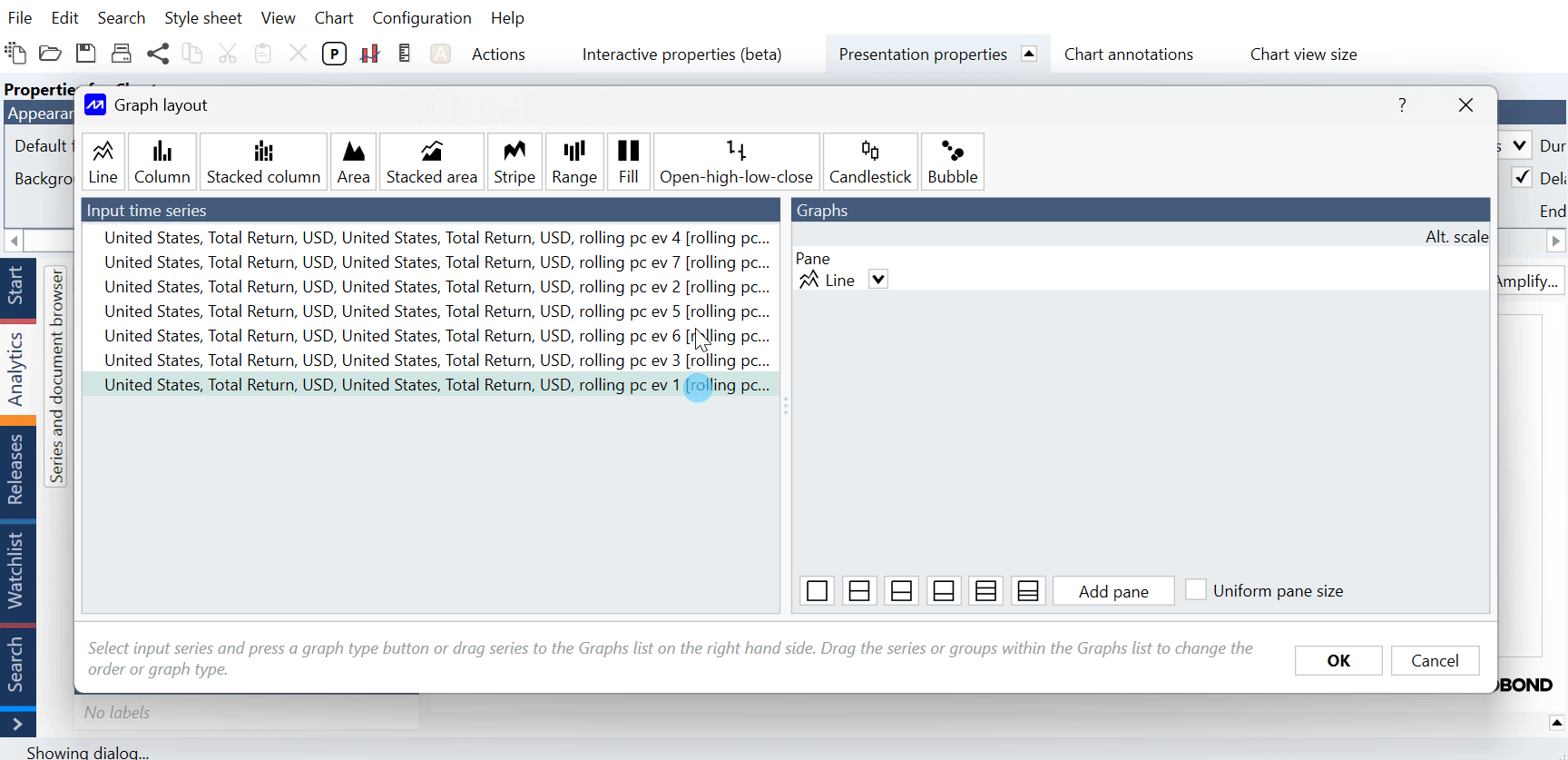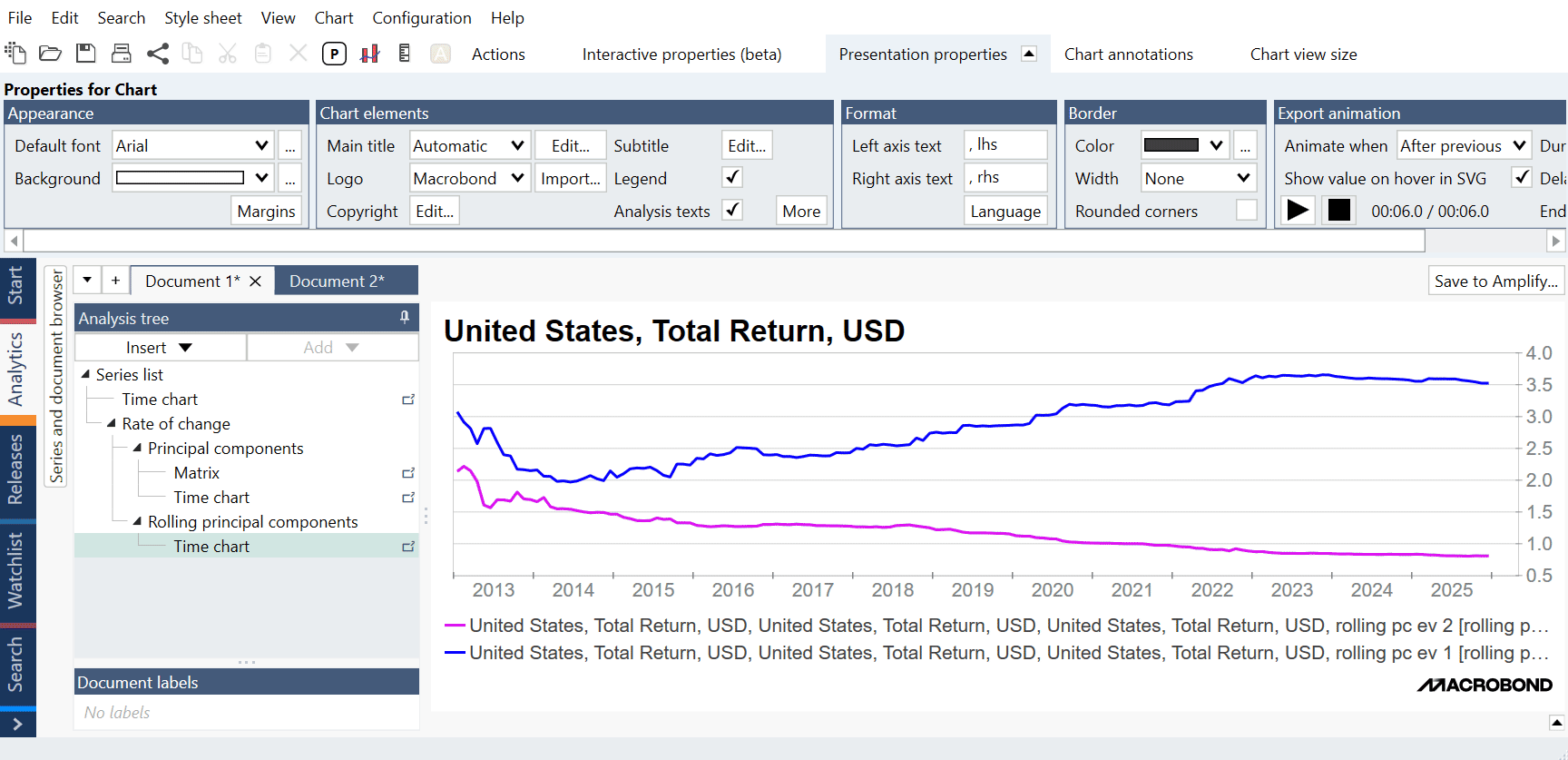
Example
In this example, we use an expanding window to determine how much systemic variance was explained by our Principal Components before and after the financial crisis. We also compare two principal components from the 'Static' PCA with the components from the Rolling PCA